PRML上巻 P15

一昨日の続き．

図に，2変数に対する同時分布の単純な例を使って，周辺分布および条件付き分布の概念を図示する． 左上の図は，同時分布からの生成を模して生成した個のサンプルデータ点をプロットしてある． 残りの図は周辺分布と，左上の図の下側の行に対応する条件付き分布のヒストグラムを表す．

%matplotlib inline

import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
np.random.seed(42)

# figure 1.11

def min_max(x: np.ndarray) -> np.ndarray:
    """min-max normalization"""
    n_min = np.min(x) - 0.001
    n_max = np.max(x) + 0.001
    return (x - n_min) / (n_max - n_min)

x = min_max(np.concatenate([np.random.normal(0.3, 0.2, 33), np.random.normal(0.7, 0.2, 27)]))
y = np.concatenate([np.random.rand(33), np.random.rand(27) + 1])

fig, axs = plt.subplots(2, 2, figsize=(12, 8))

axs[0, 0].scatter(x, y)
axs[0, 0].grid(True)
axs[0, 0].set_xticks(np.linspace(0, 1, 10))
axs[0, 0].set_yticks(np.linspace(0, 2, 3))
axs[0, 0].xaxis.set_ticklabels([])
axs[0, 0].yaxis.set_ticklabels([])
axs[0, 0].set_title('$p(X,Y)$')
axs[0, 0].set_xlabel('$X$')
axs[0, 0].set_ylabel('$Y$')

axs[0, 1].set_title('$p(Y)$')
axs[0, 1].hist(y, bins=np.linspace(0, 2, 3), rwidth=0.8, orientation='horizontal')
axs[0, 1].set_xticks([])
axs[0, 1].set_yticks([])

axs[1, 0].set_title('$p(X)$')
axs[1, 0].hist(x, bins=np.linspace(0, 1, 10), rwidth=0.8)
axs[1, 0].set_xticks([])
axs[1, 0].set_yticks([])
axs[1, 0].set_xlabel('$X$')

axs[1, 1].set_title('$p(X|Y=1)$')
axs[1, 1].hist(x[:33], bins=np.linspace(0, 1, 10), rwidth=0.8)
axs[1, 1].set_xticks([])
axs[1, 1].set_yticks([])
axs[1, 1].set_xlabel('$X$')

figure 1.11

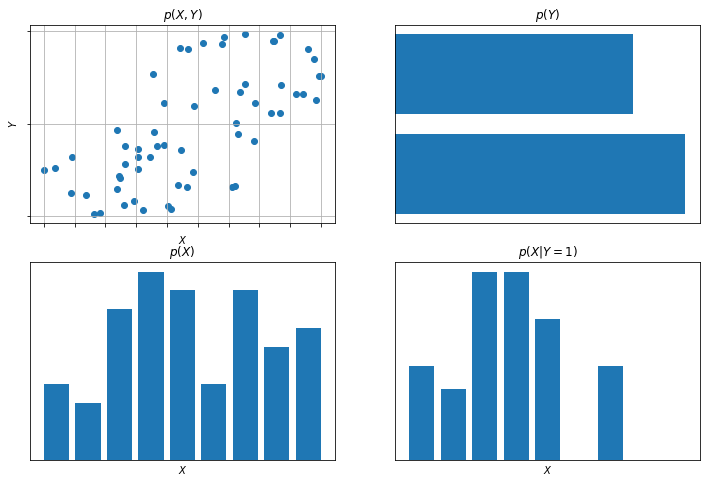
ヒストグラムは，ある確率分布から生成した有限個の点だけが与えられたとき，もとの確率分布をモデル化する単純な方法とみなすことができる．

今日はここまで．