PRML上巻 P6-7

昨日の続き．

figure 1.4

図をみると，次数のケースは関数の表現としては明らかに不適切であることがわかる． このような振る舞いは過学習(over-fitting)として知られている．

我々の目標は，新たなデータに対して正確な予測を行える高い汎化性能の達成である．

そこで汎化性能がにどう依存するかを定量的に評価する．

テスト集合に対して，誤差関数を評価する．このとき，

で定義される平均二乗平方根誤差(root-mean-square error, RMS error)を用いると便利なことがある． で割ることによりサイズの異なるデータ集合を比較できるようになり，平方根を取ることによって は目的変数と同じ尺度であることが保証される．

いろいろなに対する訓練集合とテスト集合のRMS誤差のグラフを描いてみる． ここで，テスト集合は新たに生成した100個のデータ点からなる．

%matplotlib inline
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
import numpy.polynomial.polynomial as poly
np.random.seed(42)

# t = sin(2 \pi x)
x1 = np.linspace(0, 1, 100)
t1 = np.sin(2 * np.pi * x1)
# training data set (N=10)
# t = sin(2 \pi x) + gaussian noise
x2 = np.linspace(0, 1, 10)
t2 = np.sin(2 * np.pi * x2) + np.random.normal(0, 0.2, 10)
# test data set (N=100)
# t = sin(2 \pi x) + gaussian noise
t3 = np.sin(2 * np.pi * x1) + np.random.normal(0, 0.2, 100)

RMSE_train = []
RMSE_test = []
for m in range(10):
    w = np.polyfit(x2, t2, m)
    y_train = np.poly1d(w)(x2)
    y_test = np.poly1d(w)(x1)
    E_train = 0.5 * np.sum(np.square(y_train - t2))
    E_test = 0.5 * np.sum(np.square(y_test - t1))
    RMSE_train.append(np.sqrt(2 * E_train / t2.size))
    RMSE_test.append(np.sqrt(2 * E_test / t1.size))

M = np.linspace(0, 9, 10)
p1 = plt.plot(M, RMSE_train, color='blue', marker='o', markerfacecolor='None', markeredgecolor='blue')
p2 = plt.plot(M, RMSE_test, color='red', marker='o', markerfacecolor='None', markeredgecolor='red')
plt.xlabel('M')
plt.ylabel(r'$E_{RMS}$')
plt.legend([p1[0], p2[0]], ['訓練', 'テスト'])

figure 1.5

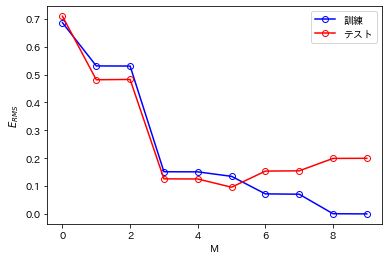
上図をみると，（書籍の図ほど顕著ではないものの）3<Mの範囲で徐々にテスト誤差が大きくなっていることがわかる．

また，では訓練誤差が0になっている．これは多項式の自由度が10であり，訓練集合の10個のデータ点にちょうど当てはめられるからである．

今日はここまで．